Date: February 3rd 2026, 15:00 – 18:00
Place: CE 1 6 and online
Schedule
15:00: Opening
15:15: Origami Bridging Art, Science, and Industry, Tomohiro Tachi
15:30: Math Advances in Origami Mechanics, Thomas Hull
15:45: Unlocking History: Origami-Inspired Virtual Unfolding of Locked Letters, Amanda Ghassaei
16:00: Rock, paper, (no) scissors … folding phlogopite and more origami lightweight engineering tales, Yves Klett
16:15: Fabricating Flat: Structural Timber Folding, Rupert Maleczek
16:30: Transformable Geodesic Gridshell by Assembling Scissor Units, Seri Nishimoto
16:45: Origami from Science to Sculpture (online), Erik Demaine
17:00: Discussion and display of models
Abstracts & short biographies
Origami Bridging Art, Science, and Industry
Tomohiro Tachi, The University of Tokyo [web]
Abstract: Folding is a fundamental principle in nature as well as the traditional art of origami and continues to inspire scientists and engineers across disciplines. In this talk, I will share my journey from crafting with paper to developing theoretical foundations, tackling computational challenges, and collaborating with experts to translate these ideas into practical applications. Additionally, I will highlight our interdisciplinary collaboration framework, bringing together artists, scientists, and students to advance both education and research.
Bio: Tomohiro Tachi is a Professor of Arts and Sciences at the University of Tokyo. He studied architecture and received his Ph.D. in engineering from the University of Tokyo in 2010. He has been designing origami since 2002 and continues to explore three-dimensional and kinematic forms through computation. He developed computational origami tools, including “Origamizer” and “Freeform Origami,” which are available on his website. His research interests include origami engineering, structural morphology, and computational fabrication. He is engaged in STEAM education at the University of Tokyo, College of Arts and Sciences.
Math Advances in Origami Mechanics
Thomas Hull, Franklin & Marshall College [web]
Abstract: Advancements in the mathematics of origami over the past 20 years have helped engineers, architects, and artists use folding in their work. In this presentation we will describe flexible 3D structures that engineers have recently been exploring and how their theory is based on a new kind of origami vertex duality.
Bio: Thomas Hull is an Associate Professor of Applied Mathematics at Franklin & Marshall College (USA). His work focuses on the many ways in which origami can be understood using math, as well as how math can be taught using origami.
Unlocking History: Origami-Inspired Virtual Unfolding of Locked Letters
Amanda Ghassaei, Independent researcher [web]
Abstract: Letterlocking is the historical practice of folding and sealing letters to function as their own envelopes, producing intricate folded letterpackets with built-in security features. This talk presents a computational approach that combines methods for simulating origami folding with x-ray microtomography to virtually unfold and read sealed historical letterpackets without opening them. This interdisciplinary collaboration demonstrates how mathematical insights from origami can be applied to the preservation and study of cultural artifacts.
Bio: Amanda Ghassaei is an independent researcher and software engineer based in Philadelphia, PA, working on computational tools for creative applications. She is currently developing PackCAD, a 3D modeling environment for origami-inspired design across packaging, engineering, and manufacturing, and has previously worked on creative tools at Adobe Research, Autodesk, and MIT.
Rock, paper, (no) scissors … folding phlogopite and more origami lightweight engineering tales
Yves Klett, Foldcore Gmbh [web]
Abstract: Origami tessellations can be put to good use in lightweight construction, especially as core structures for sandwich sheets. One feature of rigid origami tessellations like e.g. Miura-ori is that they work well for high-performance and/or fragile materials with very small breaking strains. We will present combinations of such materials with origami techniques, including structures made from high aramid and carbon fibres composites, and most recently from a mineralic paper. This phlogopite paper features comparatively low mechanical strength but excellent heat resistance and electrical insulation, and integrates very nicely into a highly fireproof origami core and non-flammable sandwich material.
Bio: Yves Klett is an aerospace engineer who started folding for his thesis and has not stopped since then. He has worked at the Institute of Aircraft Design at the University of Stuttgart researching technical tessellations, and is co-founder and managing director of Foldcore GmbH. He adapts origami structures and techniques for industrial and design applications.
Fabricating Flat: Structural Timber Folding
Rupert Maleczek, University of Innsbruck [web]
Abstract: Applying and scaling folding phenomena and strategies toward structural folding is a topic widely discussed in the Structural Origami community. This talk offers a perspective on different strategies that can be used to apply folding concepts to large-scale structures from thin wooden sheet material. A range of questions—from geometric concepts and digital fabrication constraints to hinge detailing and actuation strategies—will be discussed, and potential solutions will be shown using large-scale demonstrators developed over the last years. These structures will also help provide a perspective on scaling strategies for these principles, which are crucial for the successful implementation of these ideas.
Bio: Rupert Maleczek is an architect, researcher, and digital consultant, currently working as a postdoctoral senior scientist at i.sd (Institute of Structure and Design) in the Faculty of Architecture at the University of Innsbruck. In his multidisciplinary work, he explores the relationships among geometry, form, structure, performance, materiality, and both digital and physical production. This investigation is often grounded in the scalability of physical, geometric, and biological phenomena. The aim of his research is to understand complex relationships and enhance control over them through controlled simplification. This process, also known as simplexity, provides an accessible entry point to complex processes for non-specialists.
Transformable Geodesic Gridshell by Assembling Scissor Units
Seri Nishimoto, The University of Tokyo
Abstract: This talk introduces a “transformable geodesic gridshell” constructed by assembling elastic scissor units. When these units deform together, they cannot stay flat; instead, the structure bends out of the plane and transforms into a 3D curved surface. In this presentation, I will discuss its geometric characteristics and design principles, and show some physical models.
Bio: Seri Nishimoto is a Ph.D. student at the Department of Architecture, Graduate School of Engineering, The University of Tokyo. Her research and creative work focus on exploring the geometric properties of forms and applying them to design and fabrication.
Origami from Science to Sculpture
Erik Demaine, Massachusetts Institute of Technology [web]
Abstract: I like to blur the lines between art and mathematics, by freely moving from designing sculpture to proving theorems and back again. Paper folding is a great setting for this approach, as it mixes a rich geometric structure with a beautiful art form. Mathematically, we are continually developing algorithms
to fold paper into any shape you desire. Sculpturally, we have been exploring curved creases, which remain poorly understood mathematically, but have potential applications in robotics, deployable structures, manufacturing, and self-assembly. By integrating science and art, we constantly find new inspirations, problems, and ideas: proving that sculptures do or don’t exist, or illustrating mathematical beauty through physical beauty. Collaboration, particularly with my father Martin Demaine, has been a powerful way for us to bridge these fields.
Bio: Erik Demaine is a Professor in Computer Science at the Massachusetts Institute of Technology. Demaine’s research interests range throughout algorithms, from data structures for improving web searches to the geometry of understanding how proteins fold to the computational difficulty of playing games. He received a MacArthur Fellowship as a “computational geometer tackling and solving difficult problems related to folding and bending—moving readily between the theoretical and the playful, with a keen eye to revealing the former in the latter”. He appears in the origami documentaries Between the Folds and NOVA’s The Origami Revolution, cowrote a book about the theory of folding (Geometric Folding Algorithms), and a book about the computational complexity of games (Games, Puzzles, and Computation). Together with his father Martin, his interests span the connections between mathematics and art, including curved-crease sculptures in the permanent collections of the Museum of Modern Art in New York, and the Renwick Gallery in the Smithsonian.
Fold Our Samples!
Find here the crease pattern assignments for all the samples we are providing, along with some animations to help guide you through the folding process.
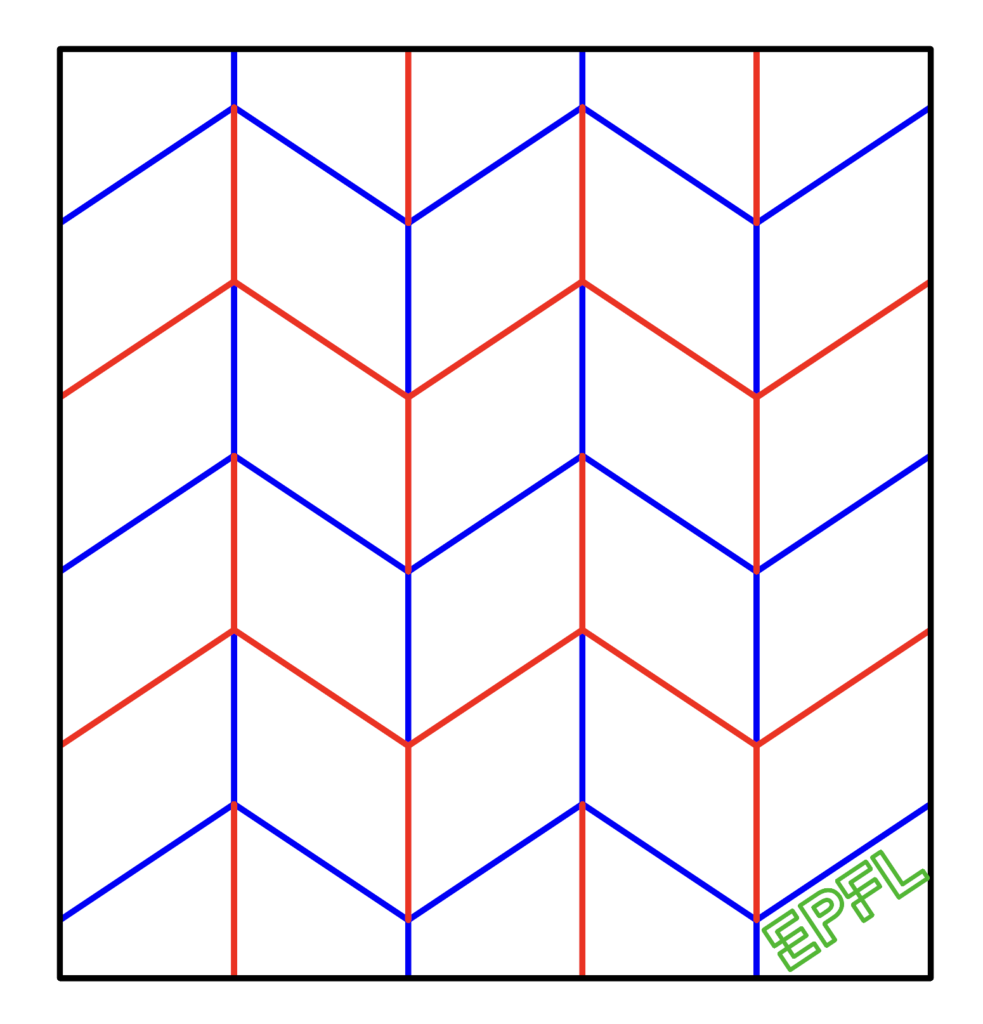
Miura Ori
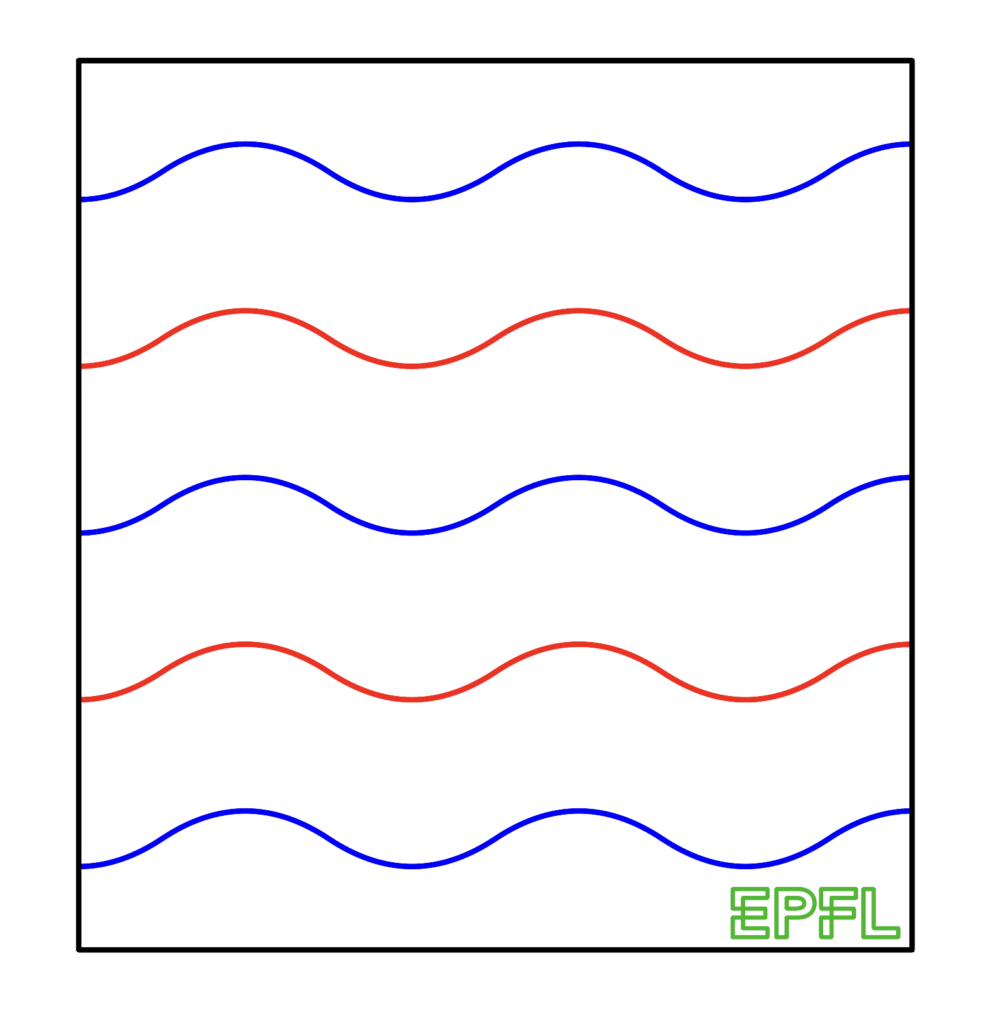
Miura Ori, but with curves.
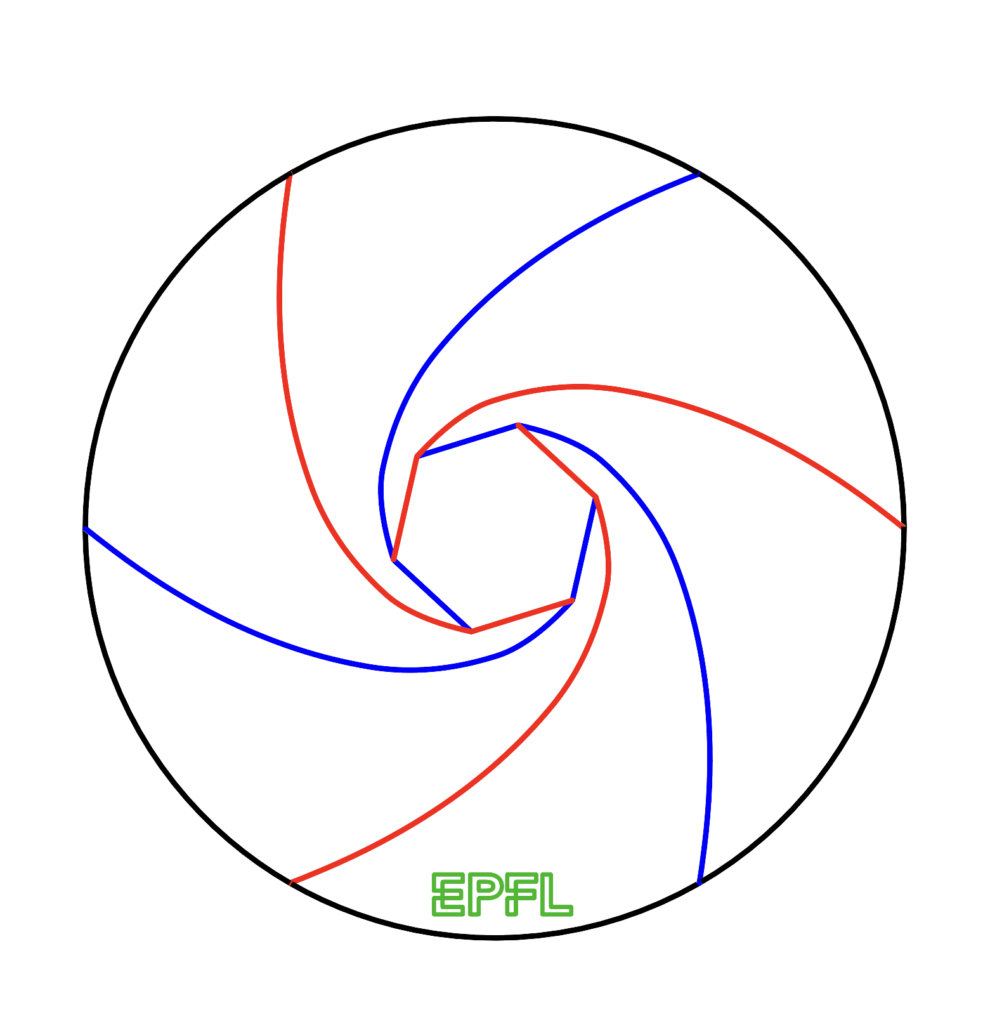
Exploded Vertex Spiral
Flasher
This one is special, as we can do the Mountain-Valley assignation in two different ways, resulting in two different shapes.
Option 1
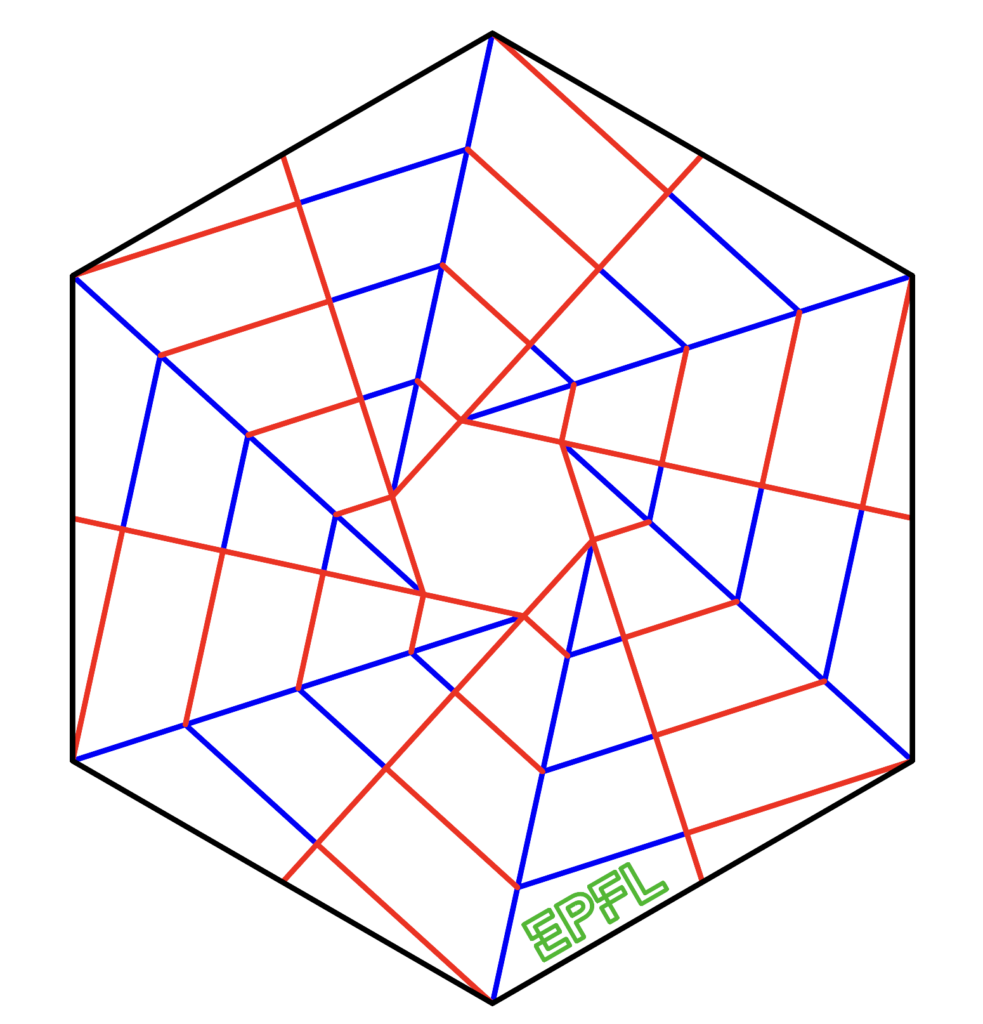
Option 2, this one leaves some creases unasigned, but that is fine and will fold!
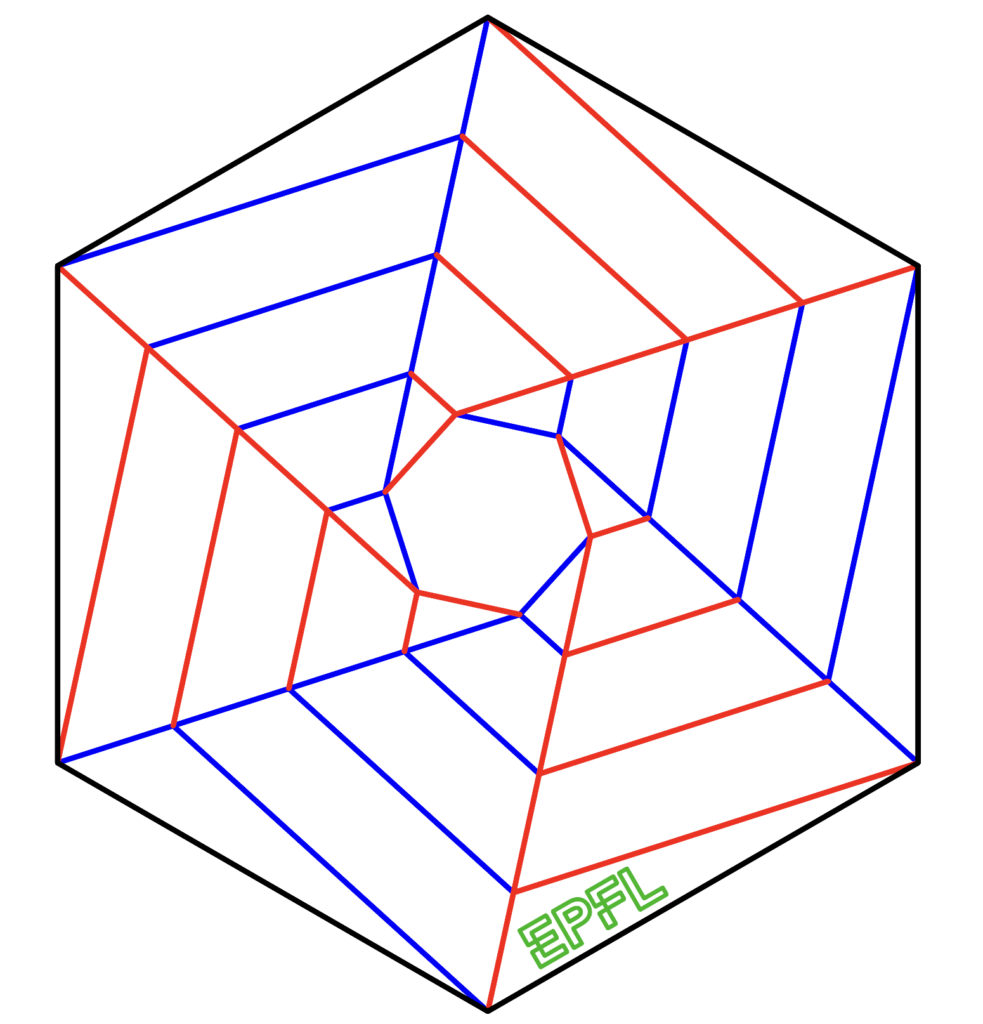
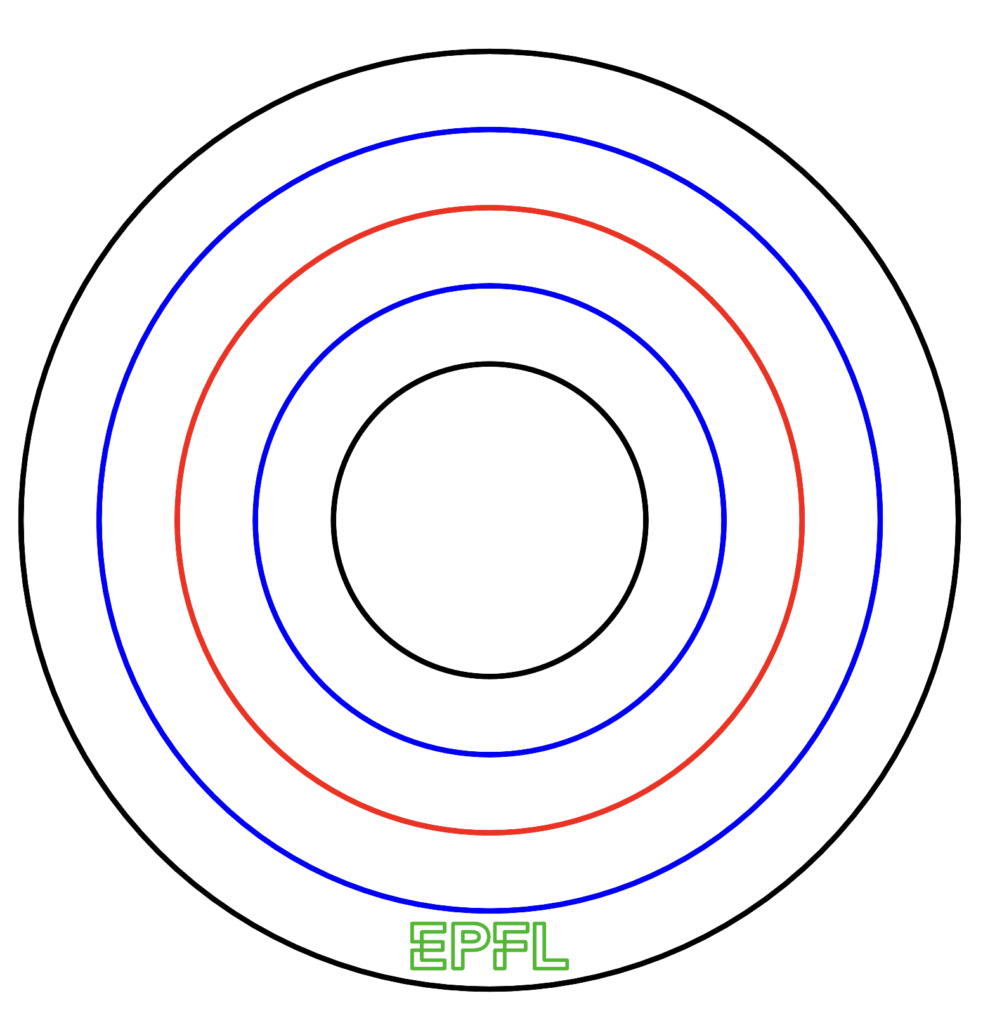
Concentric Circles
This one can be tricky to fold, but be persistent and enjoy the result.